How Many Numbers Can the Brain Store in One Second?
Quick Answer:
“Numbers stored in one second” depends on how the digits are presented and whether the brain can encode them into stable chunks. The bottleneck isn’t total brain storage—it’s attention and working memory. In most real situations, only a small amount of new digit information stays usable unless it has structure or meaning.
Searching for a simple number? You won’t find it here—because the question itself is based on a misunderstanding of how memory works. Your brain isn’t a hard drive that saves files in the first second. Instead, it’s a dynamic system where perception, attention, and encoding compete in a narrow window of time. Let’s explore what actually happens.
What This Page Explains (And What It Doesn’t)
This page focuses on the immediate cognitive processing that happens in the first second when numbers arrive. It does not cover:
- Number memory “score” norms or digit span benchmarks (see: Good Number Memory Score)
- How to improve number memory with chunking systems, PAO, loci, or the Major System
- The brain’s total storage capacity in terabytes or petabytes
- Memory athlete training techniques
Those are different questions with different answers—covered in dedicated guides.
What “Store in One Second” Actually Means
To understand the one-second limit, we need to break down three distinct processes that happen almost simultaneously:
1. Taking In (Perception)
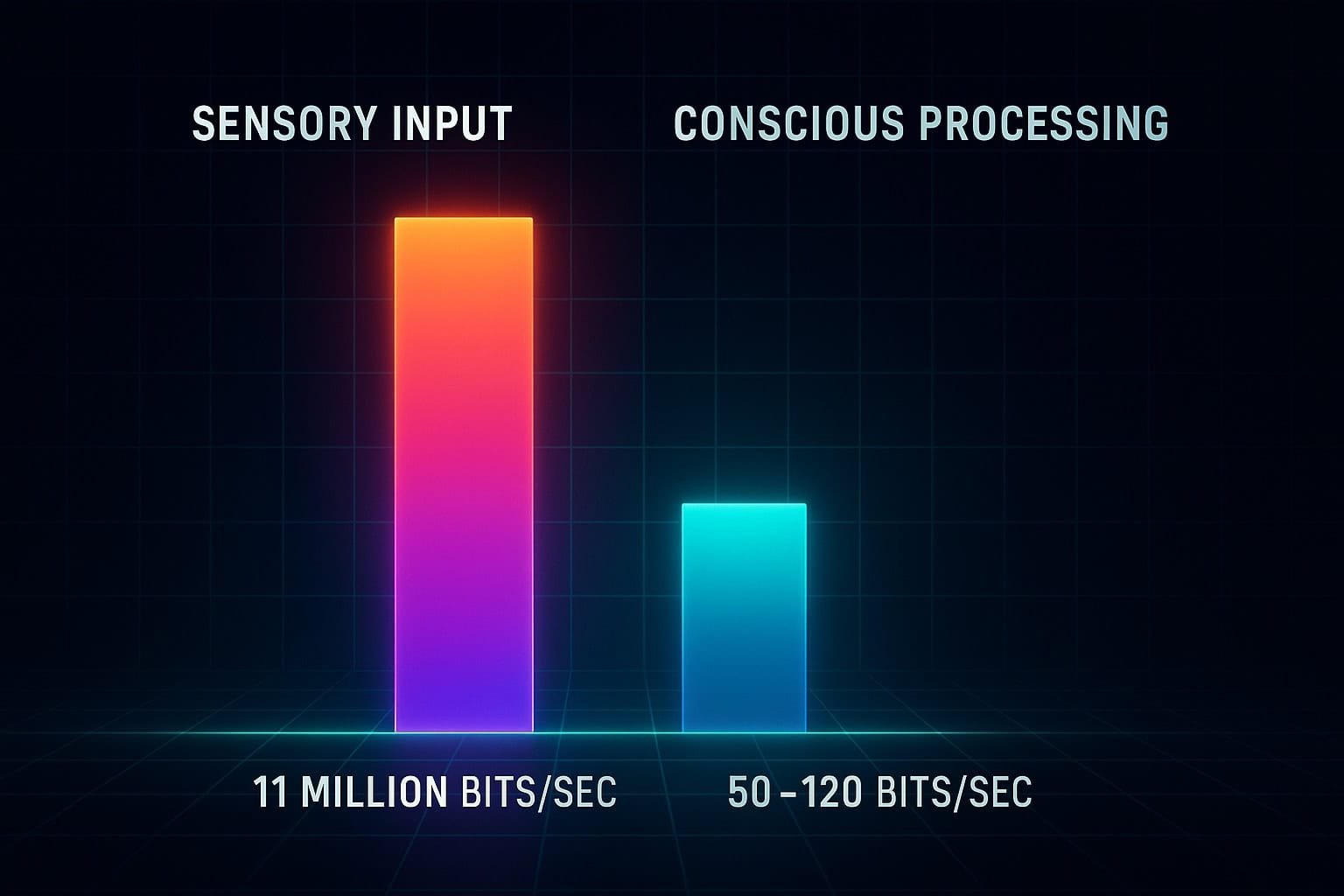
Numbers arrive as sensory data—through sight (flashed digits), sound (spoken numbers), or touch (Braille). This raw data hits a temporary buffer called sensory memory. Think of it as a high-speed, high-capacity, but extremely brief holding area. Iconic (visual) memory lasts about 300-500 milliseconds; echoic (auditory) memory lasts 3-4 seconds but starts to fade almost immediately.
2. Encoding (Stabilizing)
This is the critical bottleneck. Encoding is the process of transforming that fleeting sensory impression into a more stable neural pattern that working memory can hold. It requires focused attention. If your attention is divided or the input is too fast, encoding fails, and the information is lost before it ever truly becomes a “memory.”
3. Holding (Working Memory Availability)
If encoding is successful, the information enters working memory—your brain’s mental workspace. This is what people often mistakenly think of as “storage.” The now-famous “7±2” limit described by George Miller applies to items held here, not to what you can capture in one second. The key insight is that very little from that initial second makes it this far intact without structure or meaning.
The Real Bottleneck: Attention & Interference
Why does fast input collapse accuracy? Two main reasons:
Why “More Input” ≠ “More Stored”
Your attentional resources are finite. Presenting 20 digits in one second doesn’t mean you process 20 digits—it means you have less time (~50 milliseconds per digit) to devote attention to each one, drastically reducing the chance any will be deeply encoded. It’s like trying to read 20 billboards while driving past at high speed.
The Role of Interference
New information actively interferes with the very fragile process of encoding the information that came just milliseconds before it. This “interference effect” is a core reason why rapid serial presentation is so challenging, as shown in research on processing speed limits.
Conditions → What Typically Sticks in One Second
This table shows how different presentation formats change what’s likely to survive the one-second gauntlet:
| Input Format | What Limits Performance | What Tends to Stick | Why (The Mechanism) |
|---|---|---|---|
| Spoken digits (e.g., a quick list) | Auditory decay & attentional blink | Very little without rehearsal | Echoic memory fades; attention can’t latch onto all items sequentially. |
| Visual digits flashed briefly | Iconic memory decay & masking | A partial “impression” (3-4 items max) | Iconic memory is high-capacity but lasts less than 500 ms; a mask erases it. |
| Digits with a known pattern (e.g., 1234) | Recognition & chunking speed | The pattern as a single unit | Pre-existing knowledge allows instant chunking, bypassing slow digit-by-digit encoding. |
| Digits embedded in meaning (e.g., “911”) | Access to semantic memory | The meaning, not the digits | The brain prioritizes conceptual understanding over rote symbol recall. |
Where Working Memory Fits In
Working memory is the workspace, not the initial intake valve. The information that survives the one-second journey of perception and encoding arrives here for manipulation. Confusing its 7±2 item holding capacity with a one-second storage speed is the root of the common misconception this page corrects.
Continue Your Memory Exploration
Understanding the one-second bottleneck changes how you think about memory. To dive deeper into related concepts:
What’s a Good Score?
Learn about digit span benchmarks and what different scores mean for your working memory capacity.
Improve Your Number Memory
Explore evidence-based techniques and systems to enhance your encoding and recall over the long term.
Test Your Memory
Apply this knowledge. Take our interactive test to see how you manage numbers under time constraints.
Why Numbers Are Harder
Understand the fundamental cognitive reasons why numbers are more challenging to remember than words.
The MemoryRush Perspective
Asking how many numbers the brain stores in a second is like asking how much rain a roof catches in a storm. It’s not about the roof’s total area (the brain’s vast capacity), but the size of the gutters and downspouts (attention and encoding). Our mission is to map these gutters—the real bottlenecks of cognition—so you can understand your mind’s design and work with it, not against it. This precise, mechanistic understanding is what separates useful cognitive science from misleading pop-psychology numbers.
1 thought on “How Many Numbers Can the Brain Store in 1 Second?”
Comments are closed.